formal-notes/Formal Lang.md

Chapter 0

dont do np hard problems

Define

Computability Theory

1930s - 1950s

What can be computed?

Automata Theory

1930s - 1950s

How does making changes o the underlying model effect computational power?

Complexity Theory

1960s - Present

What is computable in practice?

P vs. NP

Graph Theory?

Define

Subgraph

Let G = \{V_G, E_G\} and H = \{V_H, E_H\}

G is a subgraph of H if

1. V_A = V_H
2. E_G \subset E_H + \forall(v_1, v_2)

Path

Hits vertices in a graph

Simple Graph: only hits vertices once

Cycle: There's some sort of loop in the graph

Simple Cycle: Only repeated node is the first and last one

Tree

Directed Graph: a graph that is made up of a set of vertices connected by directed edges

Strongly Connected: A directed graph is strongly connected if a directed path connects every two nodes.

Strings & Languages

Alphabet: Non-empty finite set

Symbol: Member of alphabet

String: Sequence of symbols

Language: Set of strings

Lecture Jan 24

idk he was talking about proofs in stuff I wasn't paying attention

Lecture Jan 27

1.1 Finite Automata

One of the simplest models of computation is the finite state machine also called finite automata

Example

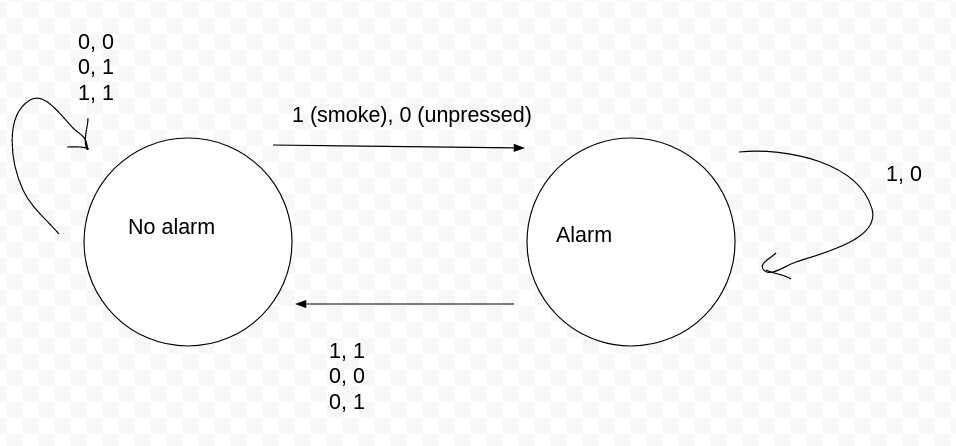
Smoke Alarm

Sensors	Values
Smoke Sensor	Smoke, No smoke
Button	Not pressed, pressed

State Diagram

!

State Transition Table

	No Smoke, unpressed	No smoke, pressed	Smoke, unpressed	Smoke, pressed
No Alarm	No Alarm	No Alarm	Alarm	No Alarm
Alarm	No Alarm	No Alarm	Alarm	No Alarm

Formal Definition of a Finite State Machine

A finite automaton is a 5 tuple (Q, \Sigma, \delta, q, F) where

1. Q is a finite set called the states
2. \Sigma is a finite set called the alphabet
3. \delta = Q \times \Sigma \rightarrow Q is the transition function
4. q \in Q is the start state
5. F \subset Q is the set of accept state

Lecture Jan 29

Define A language is called a regular language if some FSM recognizes it.

Lecture Feb 5

The transition function is taking in the current state (Q), a symbol (\Sigma), and outputs a new state (Q).

DFA - Determinant Finite Automata

\delta((q_{01}, q_2), b) = (\delta(q_{01}, b), \delta(q_2, b))

Lecture Feb 7th

!

^ NFA that accepts any string that has a zero three places from the end

Formal Definition of an NFA

An NFA is a 5 tuple (Q, \Sigma, \delta, q_o, F) where

1. Q is a finite set of states
2. \Sigma is the alphabet
3. \delta : Q \times \Sigma_\epsilon \rightarrow P(Q)
4. q_0 \in Q

Lecture Feb 10th

When reading a particular symbol a in a state R_1 our DFA simulator will apply the following the transition f^n

\delta^1(R,a) = {r \in R} | \delta(r,a)

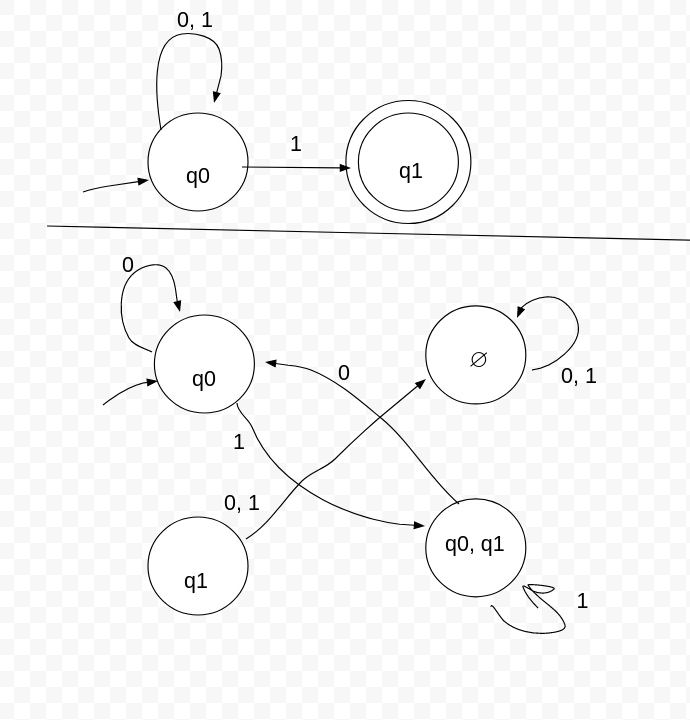
NFA to DFA example

!

Top is an NFA, lower is DFA version of it

Lecture Feb 14th

A^\star = \{x | x \in \{0, \text{None}\}\} B^\star = \{x | x \in \{1, \text{None}\}\}

Is 01 \in \{A^\star \cup B^\star \}? No. \{A^\star \cup B^\star \} = \{\{0\}^\star \cup \{1\}^\star \}

Is 01 \in (A \cup B)^\star? Yes. = (0 \cup 1)^\star A \cup B = \{0, 1\}

Empty set != empty string \{\varnothing\} \neq \{\epsilon\}